It’s no secret that analytics has had a greater impact on baseball than most, if not all other major sports. A leading reason for this is that the fundamental building block of any baseball event, a pitch, is a relatively isolated event. Sure, there are eight other players on the field, but it’s primarily a 1 vs. 1 interaction between a batter and a pitcher. Analysts covering other sports aren’t so lucky; basketball, football, soccer, and hockey all have an entire defensive staff that’s able to adjust its coverage of a player, and several teammates whose activity can have a positive or negative influence on a player’s output in hard-to-measure ways. The relative lack of outside factors influencing a pitching event, paired with the large sample size created by a long season, means that we can typically understand a player or team’s skill with a high degree of confidence.
Events in two different baseball games aren’t perfectly comparable, though. One significant factor that complicates our ability to compare one player’s performance to another’s is the ballpark factor. Unlike other sports, whose arenas have highly-regulated rules surrounding their dimensions, each baseball stadium is unique in its size and shape. Fenway Park’s center field fence is just 390ft. from home plate, while Minute Maid’s is much farther out at 436. Simply put, a home run in Boston may not have been a home run in Houston. The below image from Thirty81 Project's Lou Spirito is a nice depiction of the extreme variations between different ballparks’ dimensions (h/t Matt Monagan whose writing for Cut4 pointed me here). The full visual has a lot more detail, you can check it out here.
Climate conditions complicate this further. Some stadiums are open-air, while others can be covered. The Rockies play at an extreme altitude where the ball naturally flies farther, while the Yankees play close to sea level.
All this means that, while baseball does have the luxury of clean, 1 vs. 1 interactions whose results can be easily analyzed, we need a way to adjust for differences in venues to accurately compare one player or team’s performance to another’s.
Fortunately, the impact that a stadium has on player performance is measurable and can be applied to adjust a player’s performance to account for the stadiums they’ve played in, creating stadium-agnostic statistics. This post will be a deep dive into how these park factors work and how different stadiums measure up against each other.
Before we get started, I’ll also shamelessly plug Baseball IQ (the newsletter you’re reading right now.) If you’re interested in baseball research and analysis, consider signing up to get studies like this one delivered straight to your inbox!
The Formula
The most commonly used park factor formula is pretty simple. Here it is, from its Wikipedia page:
What’s nice about this formula is that it’s fairly easy to explain and understand. The numerator is a team’s runs scored + their opponent’s runs scored for all of their home games, divided by the total number of home games they played. The denominator is the same thing, but for the team’s road games. In short, it represents average runs scored in a team’s home stadium divided by average runs scored in their road games’ stadiums.
If a stadium is batter-friendly, we will, on average, see more runs scored in its team’s home games than in that same team’s road games. The opposite will happen if a stadium is pitcher-friendly. This means that, if 10% more runs-per-game happen in a given stadium than in an average stadium, the fraction in this formula will equal roughly 1.1. You can optionally scale this up to a 100-point scale, like the above formula does, but I typically don’t, since normalizing the values around 1 seems just as interpretable to me.
The important thing about this formula is that it’s not skewed by an individual team’s batting ability. It looks at total runs scored between both teams for a team’s home vs. away games. Over the course of a season, the skill level of the players on the field for a team’s home games vs. their away games should be pretty comparable, removing most team-level biases from this metric.
Single-Year Park Factors
Now that we have the formula, let’s apply it in the simplest way possible: to a single team’s data for a single season.
In 2019, in their 81 home games, the Texas Rangers scored 454 runs and their opponents scored 482 runs, for a total of 936 runs scored at Globe Life Field. On the road, Texas scored 356 times and their opponents scored 396 times, for a total of 752 runs scored in 81 road games. Plug this into the formula, and you get a park factor of 1.24, meaning that on average, 24% more runs were scored in the Rangers’ home stadium than in their opponents’ stadiums. We can conclude from this that the Rangers’ stadium is very batter-friendly.
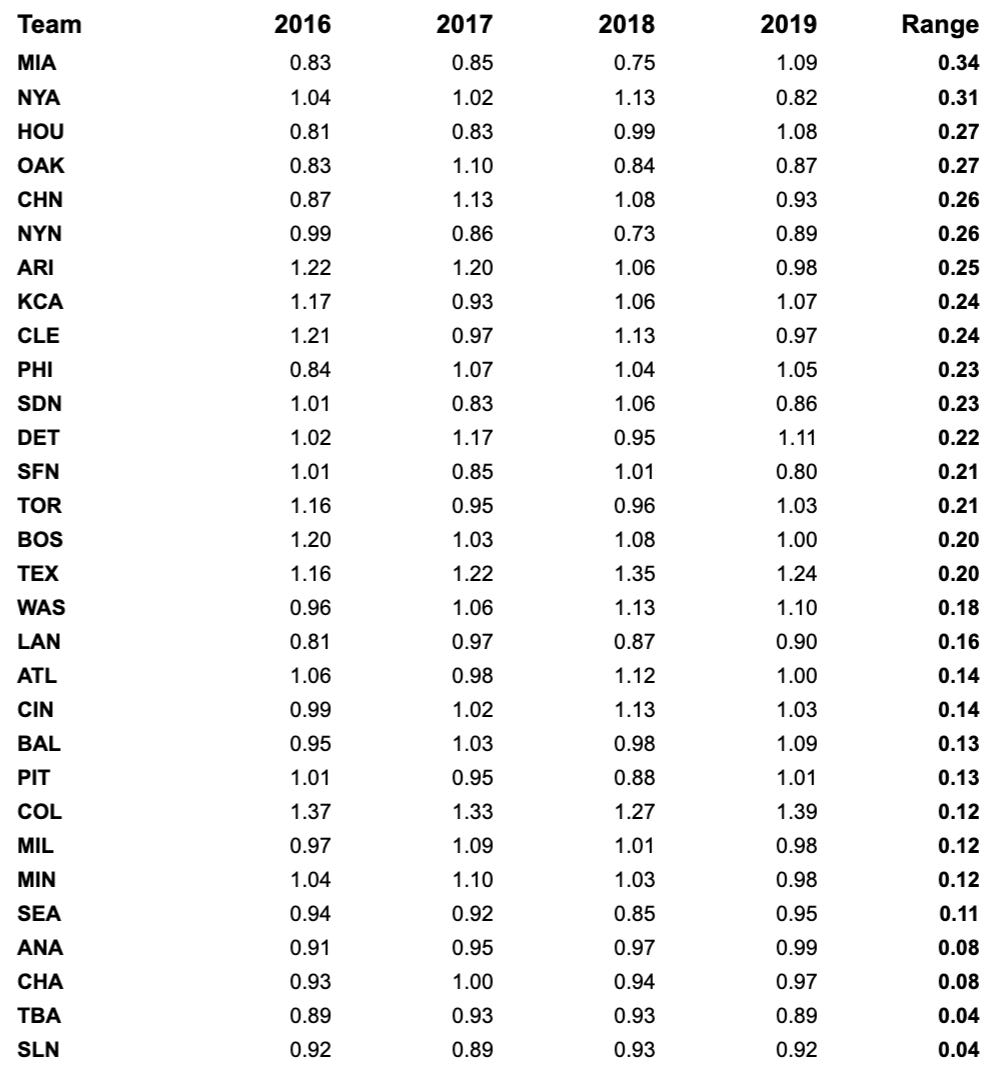
A disadvantage to these single-season effects is that they’re noisier over time than we might like. Below we see the past couple seasons’ park effects for each team. The year columns represent a team’s park factor for that season, and the “range” column represents the difference between the smallest and largest park factor for a team over this four-year period. While teams like Tampa and St. Louis have been very consistent (each year within 0.04 points of the others), we see extreme year-to-year variance for teams like the Yankees and Marlins.
We should probably assume that this variance mostly represents statistical noise, or random variation around some unknown “true” park effect. My limited research didn’t unearth any meaningful changes to the Marlins or Yankees’ stadiums from the 2018 to 2019 seasons, for example, and yet their respective park factors changed dramatically. This variance is a good reason to use the first adjustment to this formula that I’ll mention: the multi-year park factor.
Multi-Year Park Factors
It’s common to use more than one season of data to smooth over the variance in teams’ park factors from one year to the next. This doesn’t require any changes to the previously-mentioned park factor formula. Instead, we just pass it several years of runs-scored data instead of one. For the rest of this post I’ll be using three-year park factors, meaning that, for example, the Rangers’ 2019 park factor will represent runs scored from the 2017-2019 seasons instead of just the 2019 season. This adjustment makes it so these values don’t change as much from one year to the next.
Now that we have a more reliable park factor statistic, here’s 2019’s three-year park factors, sorted from most to least batter-friendly:
As you can see, there’s quite a bit of space between the most batter-friendly park (the Rockies’ Coors Field, at 1.36) and the least (the Mets’ Citi Field, at 0.82). The Rockies’ website has a nice explainer on why they’re such an outlier, which also sheds some light on other stadiums. It explains that altitude does matter, but so does wind. they say:
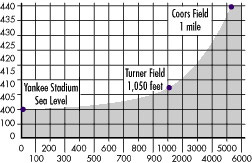
[T]he ball still travels 9 percent farther at 5,280 feet than at sea level. It is estimated that a home run hit 400 feet in sea-level Yankee Stadium would travel about 408 feet in Atlanta and as far as 440 feet in the Mile High City.
However, it's important to note that the wind can easily play a much greater role than altitude in turning fly balls into home runs. The same 400-foot shot, with a 10-mph wind at the hitter's back, can turn into a 430-foot blast. (A 10-mph wind is close to the average prevailing wind in the United States.) So, it's easy to see how a good tailwind can beat high altitude for home-run hitting any day
The altitude effect is shown in the following graphic from the Rockies’ website. The effect size isn’t huge for teams that aren’t in Denver, but it’s not nothing.
In addition to all this, holding climate constant, ballpark dimensions are the most important factor. Some stadiums are simply smaller than others, making it easier to hit a home run and therefore more batter friendly.
These multi-year park factors are usually the ones you’ll want to use to understand and adjust for the impact that a stadium has on player performance. It’s the most useful statistic for this task, with the least caveats. I will, however, go on to discuss some further adjustments we can make to this statistic that become useful under special circumstances.
Component-Level Effects
It can sometimes be useful to peek under the hood of a park factor. If we can build a single park factor representing how many excess runs a stadium generates compared to its peers, we can repeat this same procedure for any particular event.
Component-level park factors do exactly this. They’re calculated the same way as the originally-mentioned park factor formula, but instead of runs, we can swap in e.g. doubles, or home runs. This can be useful for park-adjusting a statistic like wOBA, which includes event-specific weights, or for analyzing the effect that moving to a new team will have on a player’s home run output.
Here are 2019’s three-year component-level park factors for some common stats. Remember that the “R” park factor is just the original one we’ve already been using:
Here you can compare the component-level effects for different hit types with the aggregate, more commonly-used run-level effect.
A benefit to this is that it’s far more specific than the standalone, run-level park factor. Component-level factors aren’t perfect, though. A valid concern with component-level park factors is that you’re often dealing with smaller sample sizes than with the run-level park factor. For a less common event such as triples, even a three-year park factor could be dealing with a small sample size and give deceptive results.
You should only use a component-level park factor if you have a good reason for doing so. Typically, the original park factor formula will be a better representation of what we care most about, since runs correlate closer to wins than e.g. doubles or home runs.
Handedness Splits
Everything up until this point assumes that park factors apply in a one-size-fits-all fashion to all players. We know this isn’t true. Right-handed hitters tend to drive the ball to left field, and lefties to right field. Stadiums aren’t perfectly symmetrical, so we can expect most parks to favor one direction of hitting vs. the other.
This approach is flexible enough to extend to batter handedness just like we did with component-level park factors. By simply plugging in “home runs by right-handed batters” into the original formula instead of just “runs”, we can get a right-handed home run park factor.
Below shows each team’s three-year park factors for home runs, and home runs by handedness (HR_R = home runs for righties, HR_L = home runs for lefties). The rightmost column subtracts the left-handed home run effect from the right-handed effect. Positive numbers mean a park is more home-run-friendly toward right-handed hitters, and a negative number means it favors left-handed hitters. I’m focusing on home runs here because this is the statistic most directly affected by a stadium’s outfield dimensions.
Let’s see if these handedness splits pass the eyeball test. Here are the stadiums where right handed hitters have the largest advantage over lefties (from left to right: Citi Field, Wrigley, and Nationals Park):
Notice how two of these have some sort of abnormal notch in right field, and the third seemingly has a sharper slope out toward center field’s full distance from the right field foul pole than from the left. Wrigley also has a relatively batter-friendly slope in the angle it takes from the left field line to dead center. Right-handed hitters tend to drive the ball to left field, so it makes sense that these stadiums would be better for righties than lefties.
Here are the most disproportionately lefty-friendly parks (left to right: Progressive Field, PNC Park, and Dodger Stadium).
It’s easy to see how PNC Park would disadvantage a righty with its prominent left-field notch. Progressive is noteworthy here because the deepest part of its outfield is actually pretty far into left field, as opposed to dead center. It’s harder to understand why Dodger Stadium favors lefties visually, but the numbers back it up. Maybe the rounded corners of their outfield lines aren’t as symmetrical as they look.
Last, we can take a look at the most neutral parks (left to right: Chase Field, Marlins Park, and Kauffman Stadium). Chase, in particular, is very symmetrical, with its perfectly straight center field wall.
Examples of How this Affects Batters
Let’s look at some examples of teams’ wOBA at home vs. away compared to their home park factors in 2019. Remember that wOBA is a weighted average of the run-value of several component statistics, sort of like a smarter version of OPS.
These results are a mixed bag. A lot of the results look how you’d expect (the Rangers hit better at home, the Padres hit better on the road). You do see some counter-examples, though, like Oakland’s park factor being moderately negative while the team hits slightly better at home despite this. Perhaps a home-field advantage is baked into these results, where a team may still show average batting performance at home despite it being a pitcher’s park. It’s also possible that teams adjust their staffing to account for their home park. Maybe the Pirates are more likely to sign a left-handed hitter because of PNC Park’s challenging left-field distance, for example. This local piece from Pittsburgh Sports Report certainly suggests that’s the case. I would bet that comparing road team performance to park factors gives us a significantly more clean result.
The same result can be seen with individual players, with most players’ home vs. away splits following the direction of their home park factor. Here are some cherry-picked examples of how this affected individual batters in 2019. Of course there are counter-examples, but for players in stadiums with strong park effects, you generally see their wOBA (or OBP, or OPS, or AVG) break out the way you’d expect for their home vs. away performance.
It would be interesting to see a more complete study of how home vs. away teams are impacted by park factors, and of the extent to which a team’s handedness-split park factors influence the team that they put on the field. This is already becoming a long post, so I’ll leave that to my future self or to the next person reading this.
Use Cases
A common use case for park factors is for understanding the impact that a ballpark has on a game. They help us to build our mental models of how the game works.
A more involved use case is for park-adjusting a player’s performance. You can take a player’s game-level statistics, for example, and divide each home run by the HR park factor for the ballpark he hit it in. Doing this for all players can give us a park-neutral home run leaderboard, which may become useful the next time someone from Colorado leads the league.
You could also use this to estimate how a player will perform on a new team. Say a right-handed Rockie (extreme hitter’s park) gets traded to the Cardinals (a lefty-friendly pitcher’s park). You could park adjust their previous year’s home runs in the way we’ve just described to form a park-neutral starting point, and then re-adjust them for the new ballpark by multiplying their home runs in Colorado by St. Louis’ right-handed home run park factor. The result would surely be a much lower expected home run total, since home runs in Colorado are divided by 1.26, and then to turn these neutral home runs into STL home runs, they’d again need to be multiplied by 0.80.
There are several other ways you could use these. The point is that park factors are a generic component of an analyst’s toolkit that are flexible enough to apply in many areas.
Parting Thoughts
Park factors are useful for both understanding the impact that a stadium has on batting performance and for adjusting players’ statistics into their park-neutral forms to be directly comparable with players on other teams. You can use them in their most generalizable form (multi-year, run-only effects), or you can be much more specific (component-level effects with handedness splits). The key is to be only as specific as you need to be, since adding additional layers of granularity to these adjustments can also make the data noisier and the adjustment less reliable.
The next time someone complains that a player is only performing well because of their home stadium, I hope you remember this post and that you can use park factors to remove this bias and answer such questions empirically.
Go Deeper
There’s a lot out there if you’d like to read up on more of the finer details of park adjustments or apply them in your own work. Here are some resources I like:
FanGraphs’ park factor explainer, and a deeper dive using a different formula
Book Suggestion: Analyzing Baseball Data with R (chapter 11 discusses creating your own park factors, and it’s a great resource for learning sabermetric tools and R programming in general)
Swish Analytics’ park factors, split into component- and handedness-level factors. I like the ballpark visualizations they use (example below)
If you’ve made it this far, thanks for reading! If somebody forwarded this email to you, please consider subscribing to receive my next analysis in your inbox.
If you’re already a subscriber and you like what you just read, please consider sharing Baseball IQ with a friend or tweeting this out.
Code used in writing this analysis can be found on Github here if you’d like to extend this work or create your own park factors.















Love the article! From your description of park effects, it sounds to me like the Coors Effect is significantly exaggerated. For Rockies players, the inflationary effect of hitting at Coors is at least partially mitigated by the deflationary effect of hitting on the road—ie, the negative impact of going from altitude to sea level. But, if you just take the Rockies (deflated) road scoring at face value, that would pump up the scoring advantage at Coors even further. Instead, some adjustment needs to be made for the Rockies deflated road scoring. As a result of this mistake, Nolan Arenado’s park adjusted metrics (OPS+, wRC+, etc) are much higher in St Louis than Colorado for producing similar results.